양자 컴퓨터 - 슈뢰딩거 고양이 만들기 - 파트 2: 양자 컴퓨터에 돌려보기

이전 글에서 양자 컴퓨터에서 슈뢰딩거의 고양이를 구성하는 법을 다뤘다. 유명한 슈뢰딩거의 고양이의 개념을 이용해서 큐빗(qubit)을 설명했다. 여기서는 슈뢰딩거 고양이를 실제 양자 컴퓨터로 돌려보는 것을 해본다.

IBM Q Experience에서는 양자 컴퓨터를 웹에서 클라우드로 돌려볼 수 있다. 여기서 회로를 만들거나 QASM으로 코딩을 하면 ibmqx4라는 큐빗 5개짜리 양자 컴퓨터로 내가 만든 코드가 돈다. 아주 단순한 것도 몇분 걸려서 나오니 실용적이라기보다는 테스트와 학습용이라고 볼 수 있다. 이 글에서는 IBM Q Experience를 이용해서 슈뢰딩거 고양이를 양자 컴퓨터로 돌려보도록 한다. 여기서 툴 사용법을 다 다룰 순 없으니 핵심적인 것만 다루도록 하겠다.

1. 회로 구성 및 실행

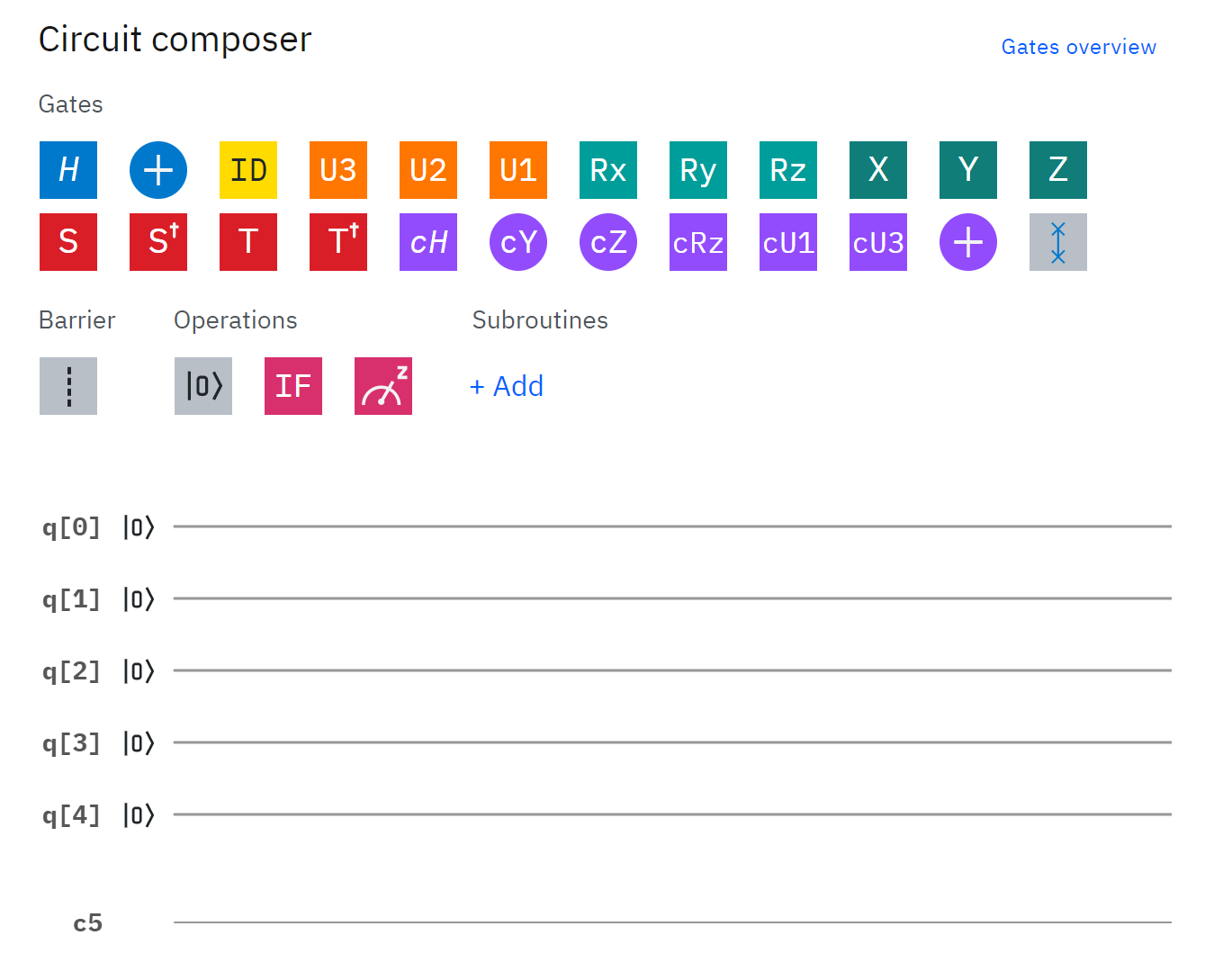그림 1. IBM Q Experience - Circuit composer

IBM Q Experience에 들어가서 Circuit composer를 열어보자. 기본적으로는 q[0]~q[4]으로 다섯개의 큐빗이 있다. 일반 고전(classical) 레지스터도 5개가 존재하며 c5로 표시되고 있다. Circuit editor에서는 QASM을 직접 수정할 수 있는데 우리는 많은 레지스터가 필요 없으니 먼저 QASM을 직접 고쳐서 다음과 같이 큐빗과 고전 레지스터를 각각 1개로 만들어보자.

OPENQASM 2.0;
include "qelib1.inc";

qreg q[1];
creg c[1];

이제 q[0]만 남았다. 그 옆에는 |0>이라는 기호가 있는데 이건 큐빗이 0 상태(state)라는 뜻이다. 입력 큐빗은 0 상태로 시작한다. 1 상태는 |1>로 표시한다. 앞선 글에서 0은 고양이가 죽은 걸 의미하고, 1은 산걸 의미한다고 했다. 죽어 있는걸 가지고 다루는게 관념적으로는 말이 안되지만 아무튼 이 서킷의 큐빗은 모두 0 상태에서 시작한다.

새로운 기호가 나왔으니 잠시 이전 글의 복습을 해보자. |0>는 고양이의 죽은 상태를 나타내는 벡터다. 벡터로는 (1, 0)로 표현했다. |1> 산 상태를 나타내고 벡터로는 (0, 1)로 표현했다. 큐빗이 0 상태로 들어온다는건 무의 상태가 들어오는 것이 아니라 (1, 0)벡터가 들어오는 것이다.

회로의 입력이 0 상태인 |0> 들어오는건 회로를 봄으로써 알고 있지만 이전 글에서 강조했던 측정을 해보자. 측정은 미터기 표시에 z 글자가 있는 아이콘(z measurement)이다. 코드로 넣을 수도 있고 드래그해서 넣을 수도 있다. 다음과 같이 구성해보자.

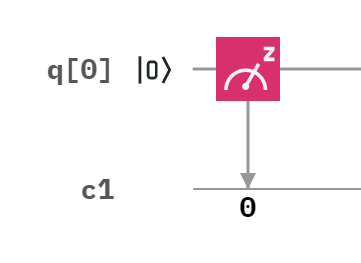그림 2. 큐빗(|0>) 측정(z measurement) 회로

여기서 아래 화살표로 0이 표시 된건 0번 고전 레지스터에 결과값을 저장한다는 의미이다. 다시 설명하면, 입력 큐빗(|0>)을 측정(z measurement)해서 0번째 고전 레지스터(c[0])에 저장한다.

이렇게 구성하고 왼쪽의 차트 모양의 아이콘을 클릭해서 Visualizations의 Statevector를 보자. 아래와 같이 에뮬레이션 된 결과를 볼 수 있다. 100%(세로 축 1)로 0 상태가 된다는 뜻이다.

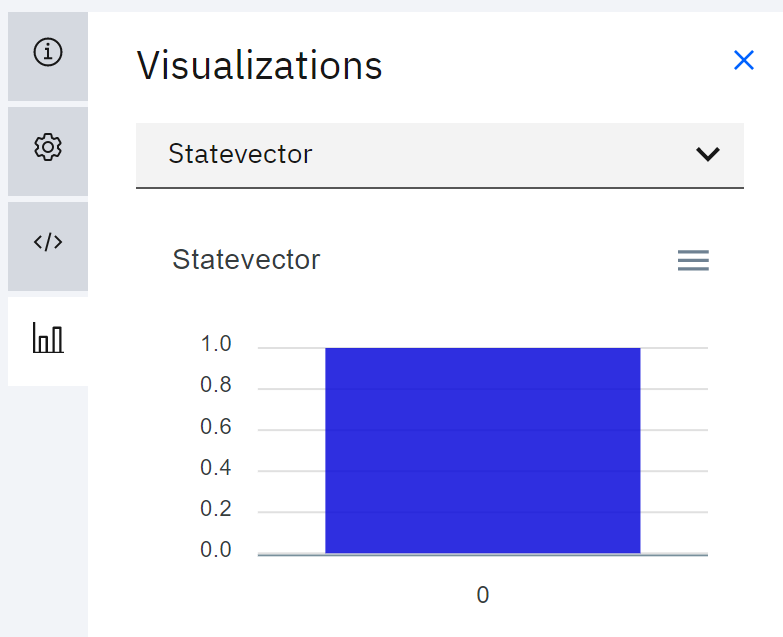그림 3. |0>의 측정 결과(Statevector)

실제 양자 컴퓨터에 넣어보자. 세이브를 하고 오른쪽 위의 Run 버튼을 누른다.

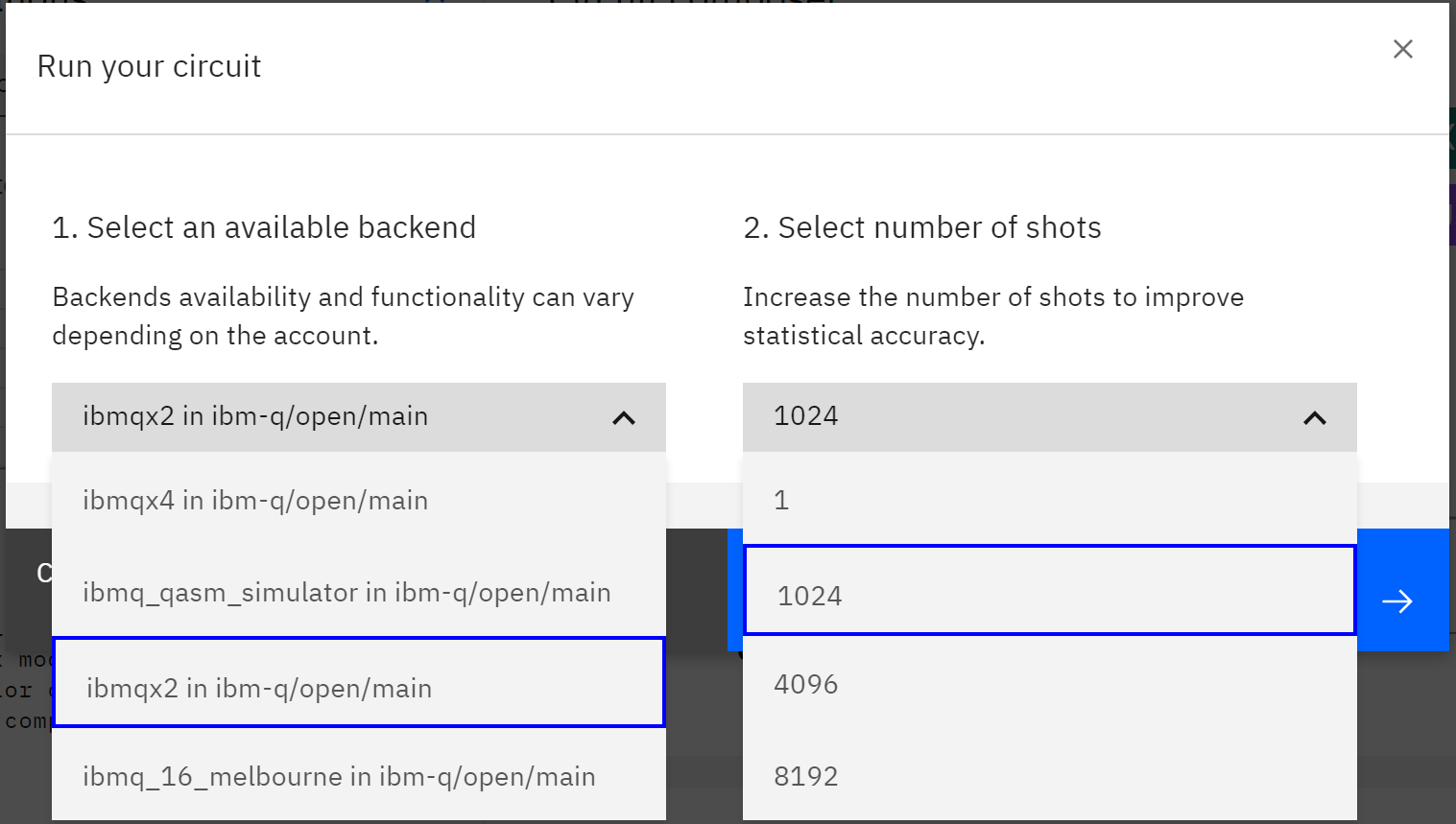그림 4. 제작한 회로를 양자 컴퓨터에서 실행

이때 굳이 4개짜리 큐빗을 쓸 필요도 없고 4천, 8천개의 실행을 돌릴 필요도 없다. 큐빗 2개 짜리인 ibmqx2 와 숫자 1024 를 고른 후 다시한번 Run 을 누른다. 그러면 화면 아래의 Pending results에 방금의 실행이 대기 상태로 들어간다. 결과는 몇분 걸린다. 1번이 아닌 몇천번의 결과를 돌리는 이유는 양자 컴퓨터의 결과는 확률적이기 때문이다. 원하는 결과가 맞는지는 확률적으로 알 수 있다.

실행을 기다리면 Status: COMPLETED가 뜨고 결과를 볼 수 있다.

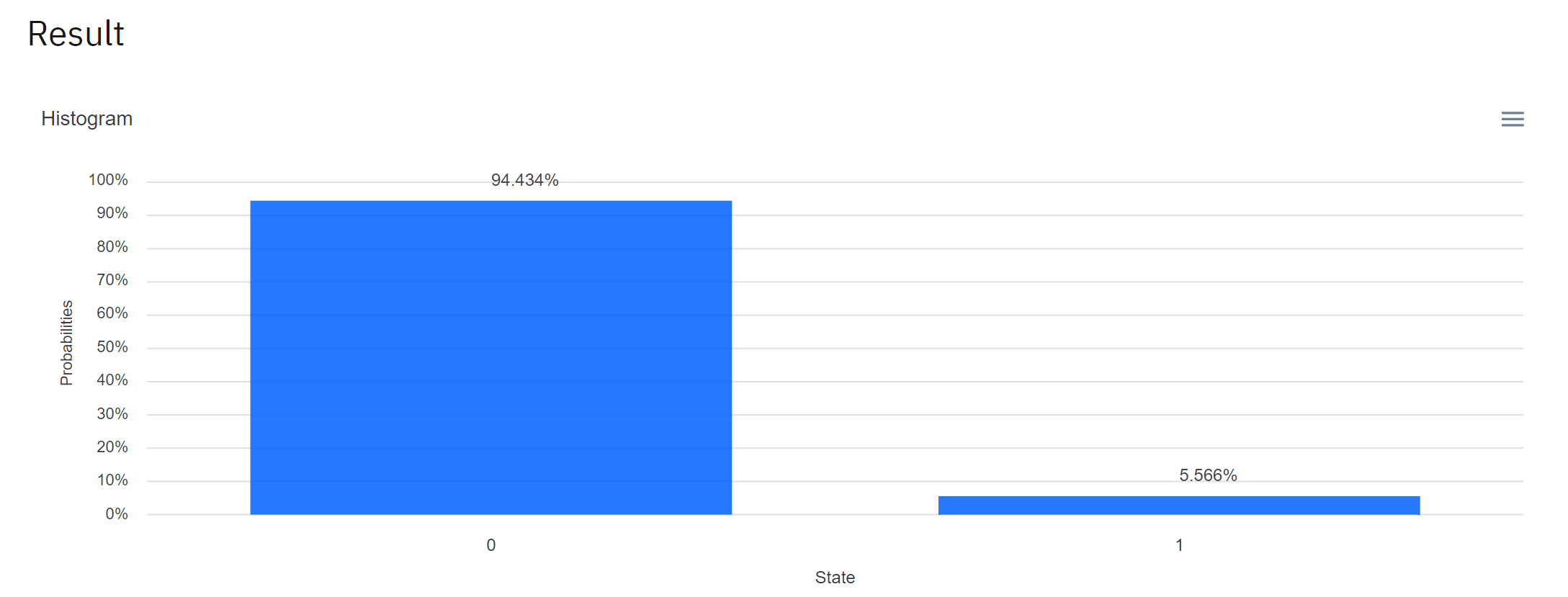그림 5. |0>을 그대로 측정한 결과. 0이 94.434%, 1이 5.566%. 이론적으로는 항상 0이 나와야 한다.

오잉? 0 상태가 100% 이어야 하는데, 94.434% 이고 1인 확률이 5.566%나 된다. 이건 현재 양자 컴퓨터의 기술적 한계로 오차는 점점 줄어 들고 있지만 아직까지는 이론적인 100%가 실제 100%이진 않다. 사실 고전 컴퓨터도 많은 오차가 있었다가 줄어든 것이고 여전히 없진 않다. 에러 검출을 이용해서 보정을 하기도 하니 양자 컴퓨터라고 딱히 비교 못할 문제가 있는 것은 아니다.

2. 슈뢰딩거 고양이 회로 만들기

이제 오차를 뒤로 하고 상태 0과 1이 각각 50%, 50%가 되는 회로를 만들기 위해 한단계 더 나아가보자.

2.1. X 게이트

큐빗의 기본 입력은 모두 |0> 이다. 이건 회로에서 다른 걸로 변환 할 수 있다. 예를 들면 0 값을 지닌 비트는 NOT 연산으로 1로 바꿀 수 있는데 이에 대응하는 것은 X 게이트라고 불리우는 Pouli X 게이트이다. X 자 아이콘으로 표시되어 있다. 이걸 측정 아이콘 사이에 넣어보자.

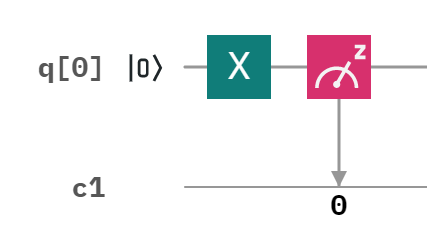그림 6. |0>에 X 게이트를 적용한 회로

아까처럼 Visualizations의 Statevector를 보면 이번엔 1 상태가 100% 인것을 볼 수 있다. 원한다면 다시한번 Run을 해봐도 좋은데 이 글에서는 다음 단계로 바로 넘어가겠다.

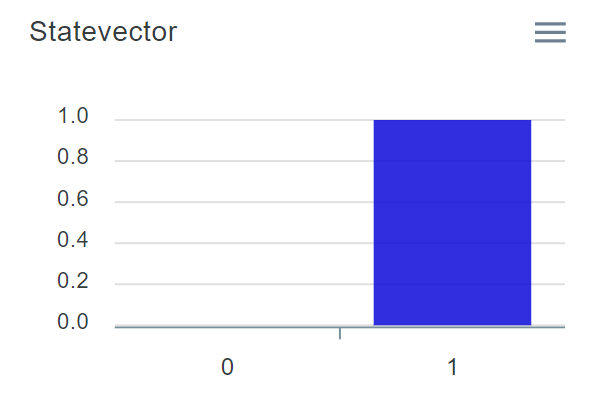그림 7. |0>에 X 게이트를 적용한 Statevector(이론적인 결과)

이렇게 하면 |0>에 X 게이트를 적용 시켜서 |1>로 바꾼다. 이걸 수식으로 표현하면 다음과 같다.

\[X|0> = |1>\]

2.2. Ry 게이트를 이용한 슈뢰딩거 고양이 회로 만들기

하지만 우리가 원하는건 |0>이나 |1>이 아니다. 50%의 값. 0.5의 확률, 이전 글에서 말한 확률 진폭으로 표현하면, \(\frac{1}{\sqrt{2}}=0.707\) 로 이 둘을 표현 해야한다. 먼저 수식으로 표현하면 다음과 같다.

\[\frac{1}{\sqrt{2}}|0> + \frac{1}{\sqrt{2}}|1>\]

|0> 을 가지고 이걸 표현하려면 Ry 라는 아이콘으로 표시 되어 있는 Ry 게이트를 사용해야한다.

\[Ry|0> = \frac{1}{\sqrt{2}}|0> + \frac{1}{\sqrt{2}}|1>\]

Ry 게이트의 진짜 역할이 뭐냐는건 이 글의 범위를 넘어가지만 기본적으로는 회전을 해주는 게이트라고 보면 된다.

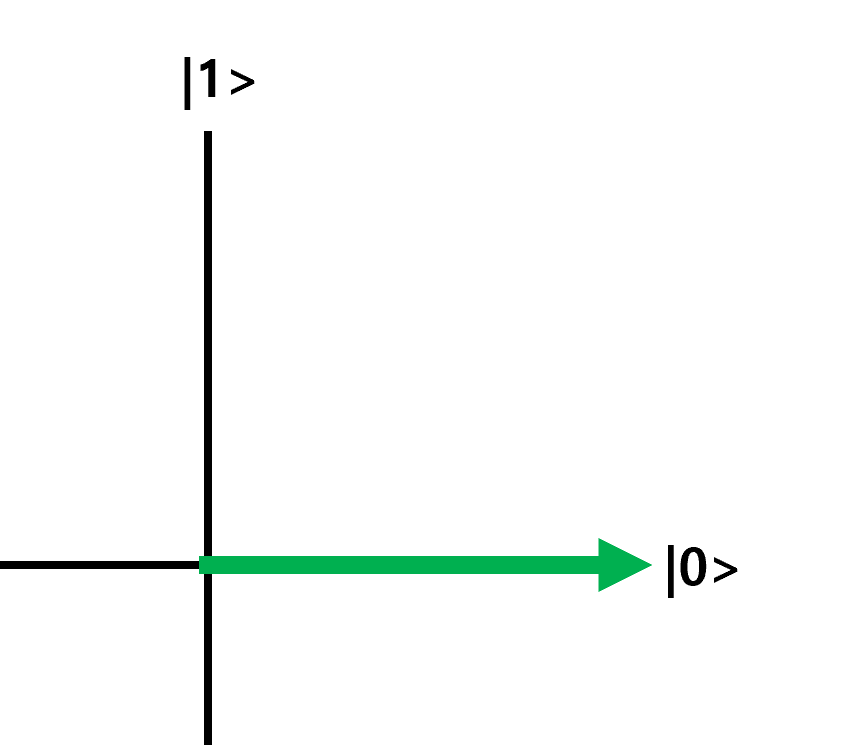그림 8. |0>을 2차원 그래프의 벡터로 표현. 이때 벡터는 길이가 1인 단위 벡터이다. 길이는 확률을 뜻한다. |0> 방향으로 길이가 1인건 |0>으로 측정될 확률이 100%라는 의미이다.

|0> 의 2차원 그래프. |0>과 |1>은 흔히 보면 xy 2차원 그래프와 비슷하게 구성할 수 있다. 그림 8에서는 |0>을 벡터로 표현했다.

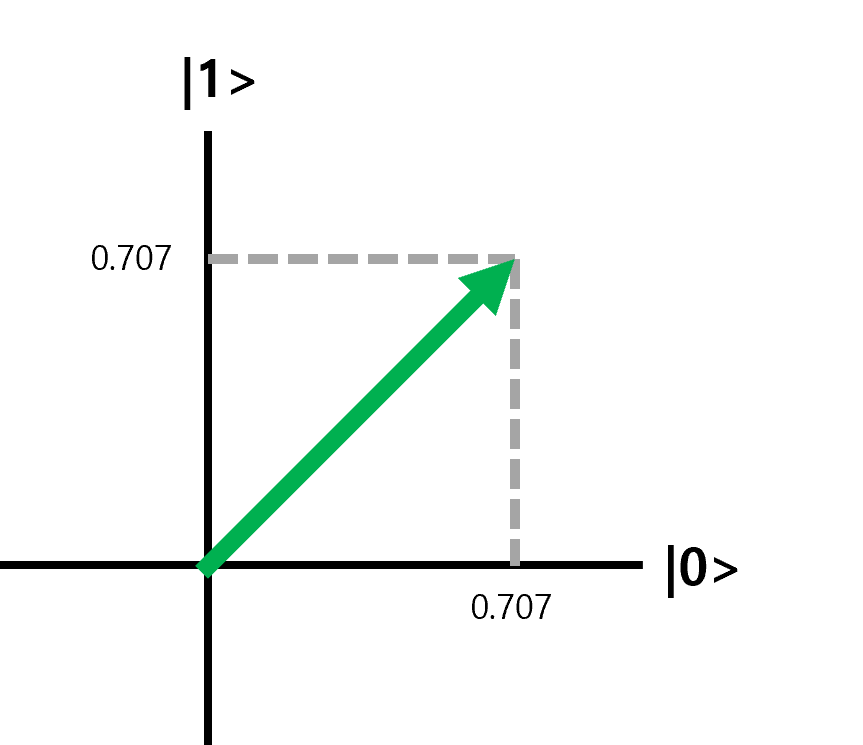그림 9. Ry|0>를 그래프로 표현. 벡터의 길이는 1인데 각 축으로의 길이는 0.707이다.

그림 9는 |0>을 Ry 게이트로 회전한 것이다. 2차원 회전하면 행렬이 생각날 수도 있는데, 실제로 맞다. X 게이트와 Ry 게이트는 모두 행렬로 표현할 수 있다. 여기서 행렬 자체를 보여주진 않겠다. 중요한건 0 상태를 Ry 게이트로 회전하면 50%, 50%를 나타내는 벡터로 변환 된다는 것이다.

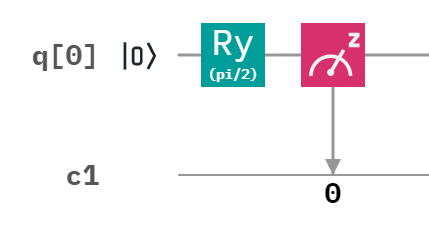그림 10. 슈뢰딩거 고양이 회로

이렇게 구성해서 Statevector를 확인해보면 0 상태와 1 상태 모두 0.707(\(=\frac{1}{\sqrt{2}}\))인걸 확인할 수 있다.

이제 Run 을 누르고 ibmqx2 와 1024를 골라서 다시 양자 컴퓨터에 실행 시켜본다.

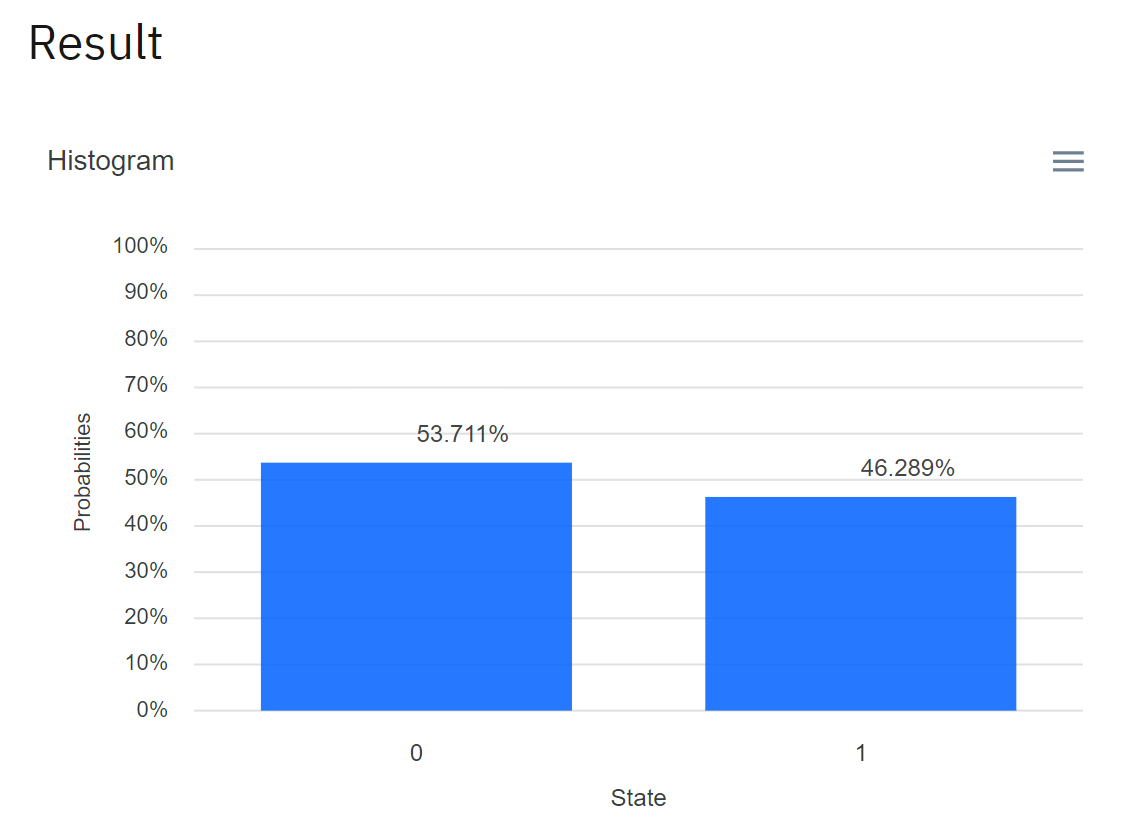그림 11. 슈뢰딩거 고양이 회로의 실제 측정 결과

이번에도 오차가 있었다. |0>일 확률은 53.711% 이고 |1>일 확률은 46.289% 이다. 오차가 크긴 하지만 이 정도면 나쁘지 않은 결과라고 할 수 있겠다.

3. 마무리

여기까지 슈뢰딩거 고양이를 나타내는 회로(그림 10)를 만들어봤다. 정확하게 말하자면 측전 전 Ry 게이트까지만 적용된 상태가 슈뢰딩거 고양이이다. 하지만 우리는 그 상태를 직접적으로 볼 수 없으므로 상자 열기라는 측정을 통해서(z measurement 아이콘) 죽은 고양이(|0>)인지 산 고양이(|1>)인지를 알 수 있게 된다.

FAQ

1. 왜 Rx 대신 Ry 를 사용한 것이며 차이는 무엇인가?

Rx 게이트를 사용해도 결과적인 확률은 같지만 계산은 약간 달라진다. 확률 진폭은 음수를 가질수도 있고 실수가 아닌 복소수로 구성되어 있다. 그래서 Ry 게이트를 사용하면 실수 확률 진폭만을 갖게 되지만,

\[Ry|0> = \frac{1}{\sqrt{2}}|0> + \frac{1}{\sqrt{2}}|1>\] \[Rx|0> = \frac{1}{\sqrt{2}}|0> - \frac{1}{\sqrt{2}}i|1>\]

Rx 게이트를 사용하면 \(\frac{1}{\sqrt{2}}\) 대신 \(-\frac{1}{\sqrt{2}}i\)를 얻게 된다. 복소수와의 관계는 설명이 너무 길어지므로 더 자세한 설명은 생략하겠다.

2. 오차가 너무 많이 난다. 오차를 줄이는 시도가 있는가?

Noise cancelling for quantum bits 영상을 보면 이러한 오차를 줄이기 위한 시도를 쉽게 설명해준다. 중간에 3D 렌더링으로 보여주는 부분도 있어서 쉽게 감을 잡을 수 있다.

3. |0>, |1> 은 생소한 표현이다.

유명한 물리학자 디락(Paul A.M. Dirac)이 만든 브라켓 표기법(bra-ket notation)으로 디락 노테이션이라고 불리우기도 한다. 복소수 벡터를 간결하게 표기할 수 있는 표기법으로 양자 컴퓨팅과 양자역학 분야에서 널리 쓰인다.

참고문헌

IBM Q Experience: 실제 코드로 돌려볼 수 있다.
IBM Q Experience로 시작하는 양자컴퓨터 프로그래밍 실습: IBM Q Experience와 QISKit(Quantum Information Software Kit)을 사용하는 방법을 설명하는 IBM의 글이다(한국어).
Noise cancelling for quantum bits
Bra–ket notation - Wikipedia