양자 컴퓨터 - 슈뢰딩거 고양이 만들기

들어가기 전

이 글은 추후에 공개 될 시리즈 글 중 한 부분이다(아마도 두번째 글). 양자 컴퓨터에 대한 간단한 소개 글을 쓰고 있는데, 그 중 이 글은 따로 떼어놓고 공개해도 될 것 같아서 미리 공개한다.

추후에 시리즈 글이 공개 될 때 다시 수정 될 수도 있고 아니면 아예 다른 글로 재작성될 수도 있다. 다만 이 글은 앞뒤 글과 무관하게 별도로 읽을 수 있어서 먼저 공개한다.

제대로 알고 알고 있는 내용들만 다루었다. 하지만 혹시나 틀린 부분들이 있을 수 있다. 댓글로 남겨주시면 매우 감사하겠다.

개요

슈뢰딩거(Schrödinger) 고양이는 일반인들도 꼭 들어봤을 법한 유명한 비유다. 슈뢰딩거의 고양이는 양자역학을 설명하는데 쓰이지만, 실제로는 에르빈 슈뢰딩거(Erwin Schrödinger)가 이게 말이 되냐고 모순점을 증명하려고 내놓은 비유다¹. 하지만 결과적으로는 응 그거 맞아인 상황이라서 이 비유를 널리 쓰게 되었다².

슈뢰딩거 고양이

그림 1. 슈뢰딩거의 고양이
출처: Shutter Stock by Sudowoodo

사고 실험이다. 어떤 독이 있다. 이 독은 기가 막히게 50%의 확률로만 고양이를 죽인다. 어떤 고양이는 면역이 있고, 어떤 고양이는 면역이 없기 때문이다. 딱 50%의 확률이다. 이때 고양이를 상자에 가두고 이 독가스를 주입한다. 그러면 50%의 확률로 살거나 죽을 것이다. 이때 상자를 미리 볼 순 없고 상자를 열어야만 우리는 고양이의 생사를 알 수 있다.

양자역학의 해석으로는 이 때 고양이는 죽은 상태와 산 상태가 공존한다. 즉, 살기도 하고 죽은 것이기도 한데 박스를 여는 순간 그 상태가 결정된다.

이게 말이 되나 싶은 얘기다. 일반적인 상식으로는 산거면 산거고 죽은거면 죽은 것이고, 박스 안 고양이는 아직 박스 안에 있기 때문에 단지 우리가 모르는 것일 뿐이다. 하지만 양자역학의 관점에서는 산 상태와 죽은 상태가 공존하고 있다는게 실험적으로 증명되었다. 물론 고양이로는 그 실험을 재현할 수 없지만, 미시적, 즉, 양자역학의 관점에서는 이미 증명되었다.

이렇게 상태가 공존하는 걸 중첩(superposition)이라고 하고, 상자를 열어서 상태를 확인하는 걸 측정(measurement)이라고 한다.

고전적(혹은 거시적) 관점에서는 측정이 대상에 큰 영향을 주지 않는다. 즉, 몰래 엿보기가 가능하다. 실험을 아주 잘 하면 실험 대상의 상태는 변하지 않는다. 하지만 양자역학 세계에서는 엿보기가 불가능하고 우리가 그걸 관찰할 때 상태가 결정 된다. 그래서 측정이 매우 중요한 역할을 한다. 이 세계에서는 측정은 엿보기가 아니라 상태를 결정 시키는 것이다. 물론 확률적으로.

동전 던지기

동전 던지기도 좋은 비유가 될 수 있다. 동전을 팽이처럼 굴린다고 하자. 시간이 지나면 동전은 회전력을 잃고 앞면이나 뒷면으로 상태가 결정 될 것이다.

고전적인 상태에서는 동전은 회전은 끝났고 이미 앞면이나 뒷면을 보이고 있는데 우리가 손바닥으로 가려서 모르고 있는 것이다. 상태는 이미 정해져있다. 우리가 모를 뿐이다. 어쩌면 몰래 엿보기도 가능하다.

반면 양자역학의 동전은 끊임 없이 회전하고 있다. 그래서 앞면일 수도 뒷면일 수도 있고 아직 결정되지 않았다. 그걸 손바닥으로 내리치면 그때 앞면이나 뒷면이 결정 된다.

비트(bit)와 큐빗(qubit)

고전 컴퓨터 데이터의 최소 단위는 비트이지만, 양자 컴퓨터의 최소 단위는 큐빗이다.

비트는 0이거나 1이다. 우리는 특정 비트의 내용을 모를 수도 있지만, 그건 우리가 모를 뿐이지 이미 메모리에 저장되어 있다. 반면 큐빗은 0인지 1인지는 아직 모르고(결정되지 않았고), 0일 수도, 1일 수도 있는 상태를 표현해야한다. 생각보다 복잡해보는데, 의외로 복잡하지 않긴 하다. 하지만…. 어.. 음.. 물론 이 글을 넘어가 나중엔 계산이 좀 복잡해진다.

양자 컴퓨터를 고전 컴퓨터로 시뮬레이션 한다고 생각해보자. 시뮬레이터를 만들어보는 이유는 그래야 고전 컴퓨터의 용어로 쉽게 설명할 수 있기 때문이다.

큐빗은 확률을 표현해야하기 때문에 1비트로는 표현이 불가능하고 실수(float, double)로 표현을 해야한다. 즉 앞면 50%, 뒷면 50%를 위해 0.5, 0.5 로 표현을 한다. 이걸 2차원 벡터로 표현해보자.

그림 2. 삶과 죽음이 중첩 된 슈뢰딩거의 고양이

\[(0.5, 0.5)\]

여기서 벡터의 앞쪽(왼쪽) 요소는 고양이가 죽을 확률(혹은 동전이 앞면일 확률)이고, 뒷쪽(오른쪽) 요소는 고양이가 살 확률(혹은 동전이 뒷면일 확률)이다. 산 확률과 죽은 확률이 동시에 존재한다.

그림 3. 슈뢰딩거의 고양이 (삶)

이때 중첩된 고양이가 아닌 위와 같이 살아 있는 고양이는 \((1, 0)\)로 표현하고

그림 4. 슈뢰딩거의 고양이 (죽음)

죽은 고양이는 \((0, 1)\)로 표현한다. 비트로 표현한다면, \((1, 0)\)은 1로 표현하고 \((0, 1)\)은 0으로 표현하면 적절할 것이다.

\((살 확률, 죽은 확률)\)로 표현하는 큐빗은 고전 컴퓨터의 비트에 대응하는 양자 컴퓨터의 최소 단위이다. 고전 컴퓨터에서 1비트로 표현하던걸 갑자기 2차원 실수형 벡터로 표현하게 되어버렸다. 너무 뻥튀기 된거 같은 느낌이 든거 같으면 정확하다. 이 때문에 양자 컴퓨터는 뭔가 대단한걸 할 수 있는 컴퓨터인거고 그만큼 만들기도 힘든 것이라고 할 수 있겠다.

결과적으로 이 글의 거창한 제목인 슈뢰딩거 고양이 만들기의 슈뢰딩거 고양이는 (0.5, 0.5) 으로 만들었다고 할 수 있다. 고양이가 살았는지 죽었는지를 0, 1의 비트가 아닌 확률로 표기된다는 점, 그 확률은 2차원 실수형 벡터로 표기한다는 점을 알면 슈뢰딩거 고양이를 만들 수 있다.

측정 (measurement)

쉽게 설명하기 위해서 좀 생략한게 있다. 큐빗은 그 자체가 확률을 가지고 있진 않다. 확율에 대응하는 확률 진폭(probility amplitude)을 가지고 있다. 확률 진폭의 절대값에 제곱을 하면³ 그게 진짜 확률이다.

그래서 실제 슈뢰딩거 고양이를 정확한 큐빗으로 표현하면 (0.5, 0.5) 대신

\[(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}})\]

으로 표현해야 한다(\(\left(\frac{1}{\sqrt{2}}\right)^2 = \frac{1}{2} = 0.5\)). 측정이란 확률 진폭을 제곱해서 확률로 바꾸고 그 확률을 토대로 상태를 결정하는 것이다.

예를 들어 만약 독가스가 80%는 살리고, 20%만 죽인다고 해보자. 그러면 이 박스 안 슈뢰딩거의 고양이는 \((\sqrt{0.8}, \sqrt{0.2}) = (0.89427, 0.4)\)으로 표현한다. 이때 박스를 열면 우리는 80%, 20%의 중첩 된 고양이는 볼 수 없고 80%의 확률로 산 고양이(1, 0)를 보거나 20%의 확률로 죽은 고양이(0, 1)를 보게 된다.

이렇게 확률 진폭을 절대값 제곱해서 확률을 얻은 확률을 가지고 상태가 큐빗을 만드는 과정을 측정한다(measuring)고 말한다. 어떤 큐빗을 가지고 있다가 상태가 뭔지를 알기 위해 측정을 하면 그에 맞는 그 확률에 맞게, 0인지 1인지가 결정 된다.

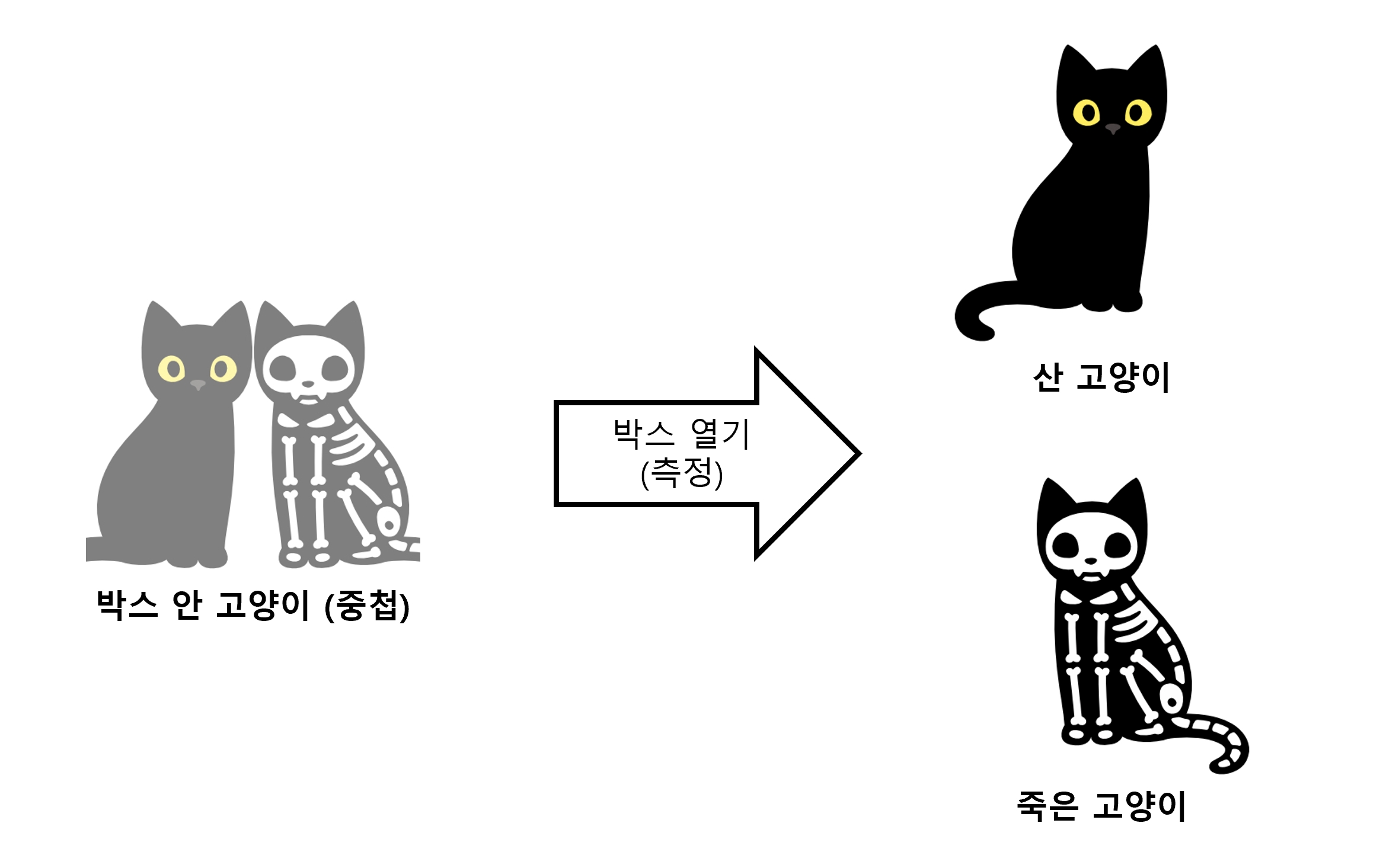그림 5.

이때 그 결정된 큐빗은 이전에 측정하기 전 큐빗과 같은 큐빗이 아니다. 측정된 상태로 변한 것이다. 다시 말해서 박스를 열고 나면(측정을 하고 나면) 이제 죽은 상태와 산 산태가 중첩 된 고양이는 존재하지 않는다. 박스를 여는 순간 이제 죽었거나 산 고양이만 남을 뿐 죽기도 하고 살기도 했던 예전의 상자 속 고양이와는 상태가 다른 고양이만 남게 된다.

마무리

이런 궁금증이 생길 수 있다. 어차피 확률 진폭과 확률이 똑같이 대응 되는 값이라면 그냥 처음부터 확률 진폭 대신 확률을 써도 되지 않을까? 그건 이 글이 다루는 범위를 넘어가는데, 실제로 양자역학이나 양자 컴퓨터에서는 확률 진폭을 가지고 직접 계산을 하는 경우가 있고, 이 경우 확률만으로는 정확한 계산을 할 수가 없다. 확률만으로 계산할 수 있었다면 양자역학이 고전적인 물리와 다르지 않았을 것이다. 확률 진폭을 가지고 계산을 하고 또 그게 완벽히 맞아 떨어지기 때문에 현대 물리는 큐빗 혹은 입자는 확률 진폭을 가지고 있다고 해석을 하고 있다.

또한 결국에는 저 중첩이라는 것이 특별한 역할을 하고 있다. 중첩을 위해서 일반 컴퓨터에서는 많은 데이터를 사용해야하는데 양자 컴퓨터에서는 중첩 자체가 자연 현상이니까 그걸 그대로 복잡한 연산에 사용할 수 있는 것이다.

참고문헌

여기서 양자역학 책을 레퍼런스로 삼으면 그렇게 적절하진 않을 것이다. 여러 책을 봤지만 Quantum Computing for Computer Scientists 책이 가장 훌륭했다. 제목대로 프로그래머를 위한 책이고, 수학/물리적인 내용들을 다 다루면서 진행한다. 이 책은 따로 리뷰 글을 남기도록 하겠다.

1. 슈뢰딩거의 고양이(Schrödinger’s cat)
2. 코펜하겐 해석(Copenhagen interpretation)
3. Quantum Computing for Computer Scientists by Noson S. Yanofsky and Mirco A. Mannucci

---