언리얼 엔진4의 PBR 머티리얼에서 스페큘러는 기본값 0.5로 0-1 범위의 값을 입력 받는다. 이런 스페큘러는 퐁 쉐이딩에서의 디퓨즈/스페큘러와는 좀 다른 개념으로 처음 PBR을 접하는 사람에게는 한번쯤은 혼돈을 주는 요소이다. 이 글은 스페큘러 0.5의 의미를 다룬 글이다. 실질적으로 PBR 작업에 도움이 될 어떤 유용한 내용을 담기보다는 PBR에서의 스페큘러의 역할과 의미가 무엇인지를 다룬다.

PBR에서 스페큘러 값은 비금속(non-metallic) 머티리얼에 대해서만 영향이 있는 값으로, 정반사 되는 빛의 양을 조절한다. 정반사 되는 빛의 양을 조절한다고하니 반사를 제어할 때 쓰일듯 하지만 실제로는 별로 그렇지 않다. 이 값을 고작 최대 8%의 반사에만 관여할뿐이고 일반적으로는 기본값인 4%의 반사 그대로두고 거의 변경하지 않는다.

다시 말해 스페큘러가 0.5 라는 것은 아래에서 설명할 4%의 반사율을 흉내내기 위한 값이다. 애매한 값이지만 그나마 0.5를 4%에 맞추면 스페큘러 값을 0-1 범위 기준으로 최대 8%의 반사율을 흉내낼 수 있다.

참고
유니티 엔진에서는 기본 PBR 머티리얼(Standard)에서는 이 값이 0.5로 고정되어 있으며 조절 불가능하다. 하지만 (비사실적이더라도) 좀 더 자유도 높은 조절을 위해서 머티리얼을 Standard (Specular setup)으로 두면 메탈릭 대신 스페큘러를 컬러로 두고 조절할 수 있다1.

스넬의 법칙 (Snell’s Law)

스넬의 법칙부터 시작한다. 물질마다 굴절률(refractive index) n 이 있고, 빛이 두 물질 사이를 지나갈 때는 스넬의 법칙에 따라 굴절 각도가 정해진다.

그림

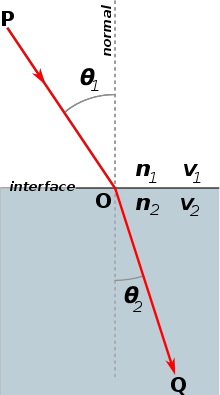
그림 1. 빛은 스넬의 법칙에 따라 굴절한다. (출처: Snell’s law - Wikipedia)

\[n_1 sin \theta_1 = n_2 sin \theta_2\]

프레넬 공식(Fresnel’s Equation)

반사에 대한 공식은 스넬의 법칙 등을 이용한 유도를 통해 프레넬 공식으로 이어지고 이어서 아래의 공식으로 이어지는데, 그 과정을 여기서는 다루지 않겠다2. 중요한것은 이때의 반사는 스넬의 법칙과 거기서 이어진 프레넬 공식을 따라 반사가 된다는 것이다. 프레넬 공식에서는 원래 편광과 투과를 고려한다.

\[R_s =\left| \frac{n_1 cos \theta_i - n_2 cos \theta_t}{n_1 cos \theta_i + n_2 cos \theta_t} \right|^2\] \[R_p =\left| \frac{n_1 cos \theta_t - n_2 cos \theta_i}{n_1 cos \theta_t + n_2 cos \theta_i} \right|^2\] \[R = \frac{1}{2}\left( R_s + R_p \right)\] \[R_0 = \left| \frac{n_1-n_2}{n_1+n_2} \right|^2\]

여기서 $R_s$, $R_p$ 는 두 편광에 대한 반사율이고, $R$이 실제 반사율이다. $R_0$ 은 입사각이 0도 일때의 반사율로, 즉, 표면에 수직으로 입사할 때의 반사률을 의미한다. 수직으로 입사하는 빛은 편광에 관한 정보가 자연스럽게 사라진다. 이제 물질의 굴절률을 알고 있으면 위 공식을 통해 수직 방향의 반사율 $R_0$을 계산할 수 있다.

PBR 에서는 수직 방향의 반사율만 다루고, 다른 방향의 반사율은 흔히 말하는 프레넬 효과로 추가해서 다룬다(프레넬 효과는 이 글에서는 더 자세하게 다루진 않는다).

진공의 굴절률(n)은 1이고, 공기는 1.000293, 물은 1.3333 정도이다. 그 외에는 유리의 굴절률은 1.52 으로, 많은 물질들의 굴절률은 1.5 안팎으로 되어 있다. 따라서 PBR 에서 공기의 굴절률은 1로 두고 유리의 굴절률은 1.5로 두면 $R_0$ 값은 0.04 로, 4%가 된다. 위에서 말한 UE4 PBR 의 4% 는 여기서 왔다.

만약 반사 되는 물질이 유리가 아닌 다른 물질이라면 여기서 스페큘러를 약간 변경된 값으로 사용하면 된다.

예를 들면 다이아몬드는 2.42로 R_0는 17% 정도 되는 큰 값이고, 얼음은 1.31 으로 얼음에 해당하는 $R_0$ 는 2% 이다. 다이아몬드는 좀 큰 값이지만 흔히 보는 대부분의 물질들은 1.5 근처에 있다. 플라스틱의 굴절률은 일반적으로 1.3~1.7 정도로, 1.5면 평균적인 값으로 쓰기 좋다3.

[표] 물질별 굴절률에 따른 반사율과 스페큘러(파장 $\lambda=589 nm$)

물질 굴절률 반사율 스페큘러
유리 1.52 4.3% 0.53
얼음 1.31 2% 0.25
산화알루미늄 1.77 8% 0.97
다이아몬드 2.42 17% 2.15 (UE4에서 입력 불가능)

아래에 직접 굴절률을 입력하면 반사율과 스페큘러를 계산해서 보여주도록 만들어봤다.

굴절률(n):
반사율($R_0$):
스페큘러: (0~1의 범위)

정리

정리 1

  • 많은 비금속 물질의 반사율은 4%에 가깝다.
  • 반사율은 물질의 굴절률에 따라 다르지만 1.5 정도로 맞추면 많은 물질과 비슷하게 생각할 수 있다. 이때 굴절률 1.5에 해당하는 것이 4%다.
  • 반사율은 입사각에 따라 다르지만, 수직으로 입사하는 빛(입사각=0)의 4%를 기본으로 하고 비스듬한 방향에서의 반사는 프레넬 효과로 처리한다.

그림

그림 2. 녹색 화살표는 4%를 의미하고, 녹색 사각형은 프레넬 효과가 담당하는 영역을 의미한다.
(이미지 출처: Fresnel equations - Wikipedia)

정리 2

  • UE4 에서는 (비금속의) 반사율을 0~8%로 제한한다. 스페큘러 0.5 값이 기본값 4%에 해당한다.
  • 유니티에서는 기본적으로는 0.5로 고정된 값을 변경할 수 없지만,
  • 머티리얼을 Standard (Specular setup)로 두면 금속/비금속 설정 대신 스페큘러 설정을 자유롭게 변경할 수 있다.
  • 즉, 금속/비금속의 차이는 근본적으로 이 스페큘러의 차이에 있다.

그러면 금속/비금속이 왜 나뉘고, 왜 비금속은 반사율이 4% 남짓 되는 작은 값 밖에 안되느냐가 궁금해질 수 있다. 그건 다음 이시간에.

출처 및 참고

  1. 이때 스페큘러 컬러의 기본값은 (51/255, 51/255, 51/255)인데, 이것은 감마 공간의 값이라 이것을 선형 공간으로 변형하면 (51/255)^1/2.2 대략 0.5의 값이 나온다. ↩

  2. 프레넬 공식의 유도는 검색해도 쉽게 찾을 수 있는데, 편광과 자기장의 요소 때문에 간단하게 설명하긴 쉽지 않다. ↩

  3. 사실 이 굴절률은 빛의 파장(색깔)에 따라 또 다르다(위 값들은 파장 589 nm 기준이다). ↩